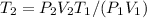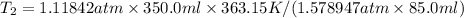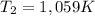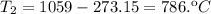Answer:

Step-by-step explanation:
Ideal gases follow the combined law of gases:

Where,
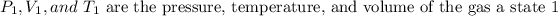
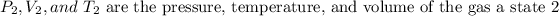
- Pressure is the absolute pressure and its units may be in any system, as long as they are the same for both states.
- Also, volume may be in any units, as long as it they are the same for both states.
- Temperature must be absolute temperature, whose unit is Kelvin.
Your data are:
- P₁ = 1200.00 mmHg
- P₂ = 1.11842 atm
- V₁ = 85.0 mL
- V₂ = 350.0 mL
- T₂ = ?
- T₁ = 90.0ºC
1. Conversion of units:
- P₁ = 1200.00 mmHg × 1.00000 atm / 760.000 = 1.578947 mmHg
- T₁ = 90.00ºC + 273.15 = 363.15K
2. Solution
- Clearing T₂, from the combined gas equation you get: