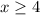Answer:
The piecewise model of the function is
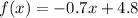 -----> For
-----> For
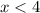
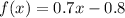 -------> For
-------> For
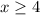
Explanation:
we know that
The general form of absolute value equation is
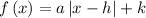
where
The variable a, tells us how far the graph stretches vertically, and whether the graph opens up or down
(h,k) is the vertex of the absolute value
In this problem we have
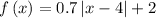
we have
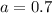
The coefficient a is positive ----> the graphs open up
The vertex is the point (4,2)
Find the piecewise model
case 1) positive value
![f(x)=0.7[(x-4)]+2](https://img.qammunity.org/2021/formulas/mathematics/middle-school/nvm80dncg2l9fdqheeq09ptufi8s23v550.png)
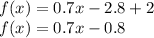
Is a linear equation with positive slope
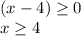
The domain is the interval [4,∞)
case 2) negative value
![f(x)=0.7[-(x-4)]+2](https://img.qammunity.org/2021/formulas/mathematics/middle-school/axi4rnjj4zkhthc6cr5lob13shd39t591m.png)
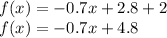
Is a linear equation with negative slope
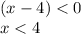
The domain is the interval (-∞,4)
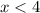
therefore
The piecewise model of the function is
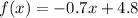 -----> For
-----> For
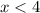
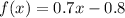 -------> For
-------> For