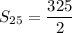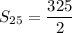
Explanation:
The given sequence:
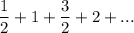
Here, first term (a) =
 , common difference(d) =
, common difference(d) =
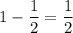 and
and
the number of terms (n) = 25
The given sequence are in AP.
To find, the value of
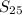 = ?
= ?
We know that,
The sum of nth terms of an AP
![S_(n)=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2021/formulas/mathematics/high-school/vatoeise4f29ho7ec2u4lj83odu5s2s51h.png)
The sum of 25th terms of an AP
![S_(25)=(25)/(2)[2((1)/(2))+(25-1)((1)/(2))]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ypzlps352h8wu24uatjjrnithrstlidw4e.png)
⇒
![S_(25)=(25)/(2)[1+(24)((1)/(2))]](https://img.qammunity.org/2021/formulas/mathematics/high-school/5k9uhw16j3xnknebr221z027ln9sghqxik.png)
⇒
![S_(25)=(25)/(2)[1+12]](https://img.qammunity.org/2021/formulas/mathematics/high-school/xtk1dwe63w11uhyq57qhtkxro3qyaja0zv.png)
⇒
![S_(25)=(25)/(2)[13]](https://img.qammunity.org/2021/formulas/mathematics/high-school/x3wxw6zun98ggrqxvdjrteyumrypft42ox.png)
⇒
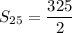
∴