Question

A tennis ball has a mass of 0.059 kg. A professional tennis player hits the ball hard enough to give it a speed of 41 m/s (about 92 miles per hour.) The ball moves toward the left, hits a wall and bounces straight back to the right with almost the same speed (41 m/s).

A) What is the average speed of the ball during the period from first contact with the wall to the moment the ball's speed is momentarily zero?
B) How much time elapses between first contact with the wall, and coming to a stop?
C) What is the magnitude of the average force exerted by the wall on the bal dring contact?
D) In contrast, what is the magnitude of the gravitational force of the Earth on the ball?

Answer 1

The average speed of the tennis ball during contact with the wall is zero, and without the time of contact, we cannot determine the time elapsed or the average force exerted by the wall. However, the gravitational force on the ball is 0.5782 N.

Step-by-step explanation:

The question relates to the change in momentum and the forces involved when a tennis ball bounces off a wall. Specifically, a tennis ball with a mass of 0.059 kg is hit at a speed of 41 m/s, bounces off a wall, and comes back at the same speed. To tackle the posed questions, it is essential to apply concepts from Newton's laws of motion and the conservation of momentum.

Part A

The average speed of the ball during contact is zero since the speed decreases uniformly from 41 m/s to zero.

Part B

Without the time of contact with the wall, this cannot be determined. Previous examples of collisions show time of contact can vary, so it must be provided to answer this part of the question.

Part C

To calculate the magnitude of the average force exerted by the wall on the ball, we would need the time of contact with the wall. Since it is not given, this cannot be calculated accurately.

Part D

The magnitude of the gravitational force of the Earth on the ball is calculated as the product of the mass of the ball and the acceleration due to gravity (9.8 m/s²), which is 0.059 kg * 9.8 m/s² = 0.5782 N.

Answer 2

There is an omission of some sentences in the question which affects the answering of question B and C, so we will based the omission of the sentences on assumption in order to solve the question that falls under it.

NOTE: The omitted sentences are written in bold format

A tennis ball has a mass of 0.059 kg. A professional tennis player hits the ball hard enough to give it a speed of 41 m/s (about 92 miles per hour.) The ball moves toward the left, hits a wall and bounces straight back to the right with almost the same speed (41 m/s).

As indicated in the diagram below, high-speed photography shows that the ball is crushed about d = 2.0 cm at the instant when its speed is momentarily zero, before rebounding.

A) What is the average speed of the ball during the period from first contact with the wall to the moment the ball's speed is momentarily zero?

B) How much time elapses between first contact with the wall, and coming to a stop?

C) What is the magnitude of the average force exerted by the wall on the bal dring contact?

D) In contrast, what is the magnitude of the gravitational force of the Earth on the ball?

Answer:

a)
`V_(avg) = 20.5m/s`

b) 9.76 × 10⁻⁴s

c) 247.9 N

d) 5.8 N

Step-by-step explanation:

Given that;

Initial speed
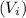`(V_i)` = 0

Final speed
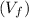`(V_f)` = 41 m/s

Distance (d) = 0.002

mass (m) = 0.059 kg

g = 9.8 m/s²

a)

The average speed of the ball can be calculated as;

`V_(avg) = (V_i+V_f)/(2)`

`V_(avg) = (0+41)/(2)`

`V_(avg) = 20.5m/s`

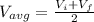
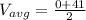
b)

The time elapsed can be calculated by using the second equation of motion which is given as:

`S=((V_i+V_f)/(2))t`

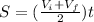
If we make time (t) the subject of the formula; we have:

`(V_i+V_f)t=2S`

`t= ((2S)/(V_I+V_f))`

`=(2(0.02))/(41+0)`

`=(0.04)/(41)`

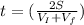
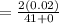
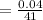
= 0.000976

=9.76 × 10⁻⁴s

c)

the magnitude of the average force (F) exerted by the wall on the bal dring contact can be determined using;

Force (F) = mass × acceleration

where acceleration
`(a)= (Vo)/(t)`

`(41)/(0.00976)`

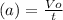
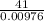
acceleration (a) = 4200.82 m/s²

F = m × a

= 0.059 × 4200.82

= 247.85

≅ 247.9 N

d)

the magnitude of the gravitational force of the Earth on the ball

Force (F) = mass (m) × gravity (g)

= 0.059kg × 9.8 m/s²

= 5.782 N

≅ 5.8 N