Question

How you should answer:

1. Known:

2.Unknown:

3.Rationle:

4.Equation and Solution:


Steps on how to answer:

-State the known

-State the unknown and represent it with a variable

-Provide a rationale for your approach

-Include the equation, exact answer, and decimal approximation

Answer 1

Question 1

Focus on the triangle on the left.

sine is the ratio of opposite over hypotenuse

sin(angle) = opposite/hypotenuse

sin(44) = w/30

w = 30*sin(44)

w = 20.839751 approximately

Now move onto the triangle on the right. We'll use cosine this time.

cos(angle) = adjacent/hypotenuse

cos(x) = w/45

cos(x) = 20.839751/45

cos(x) = 0.463106

x = arccos(0.463106) ... arccosine is the same as
`\cos^(-1)`

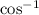
x = 62.412286

Answers:

w = 20.839751 approximately

x = 62.412286 approximately

==========================================================

Question 2

Focus on the triangle on the left.

sin(angle) = opposite/hypotenuse

sin(32) = w/5

w = 5*sin(32)

w = 2.649596

Now move to the triangle on the right.

sin(angle) = opposite/hypotenuse

sin(x) = w/5

sin(x) = 2.649596/5

sin(x) = 0.5299192

x = arcsin(0.5299192) .... arcsine is the same as
`\sin^(-1)`

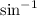
x = 31.999996

Answers:

w = 2.649596 approximately

x = 31.999996 approximately

==========================================================

Question 3

This time we use the tangent ratio.

Focus on the triangle that has legs of w and 16.

tan(angle) = opposite/adjacent

tan(70) = 16/w

w*tan(70) = 16

w = 16/tan(70)

w = 5.823524

Now let y = x+w and focus on the largest triangle this time.

tan(angle) = opposite/adjacent

tan(41) = 16/y

y = 16/tan(41)

y = 18.405895

This leads to:

y = x+w

x = y-w

x = 18.405895 - 5.823524

x = 12.582371

Answers:

w = 5.823524 approximately

x = 12.582371 approximately