Question

A 3.42 kg mass hanging vertically from a spring on the Earth (where g = 9.8 m/s2) undergoes simple oscillatory motion. If the spring constant is 12 N/m, find the period of oscillation of this setup on the moon, where g = 1.6 m/s2.

Answer 1

Time period of oscillation on moon will be equal to 3.347 sec

Step-by-step explanation:

We have given mass which is attached to the spring m = 3.42 kg

Spring constant K = 12 N/m

We have to find the period of oscillation

Period of oscillation is equal to
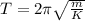`T=2\pi \sqrt{(m)/(K)}`, here m is mass and K is spring constant

So period of oscillation
`T=2* 3.14* \sqrt{(3.42)/(12)}`

`T=2* 3.14* 0.533=3.347sec`

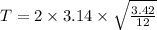
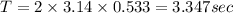
So time period of oscillation will be equal to 3.347 sec

As it is a spring mass system and from the relation we can see that time period is independent of g

So time period will be same on earth and moon