Question

!!! need help!! whats the answer??

Answer 1

i) Therefore option A is Correct. Δ ECD
`\sim` Δ ACB by the SAS ( Side Angle Side) Similarity Theorem.

ii) Yes it can be proven that ED || AB after proving that Δ ECD
`\sim` Δ ACB

Explanation:

i) CE =
`(1)/(2)` AC ..... given

ii) CD =
`(1)/(2)` CB .... given

iii) Therefore
`(CE)/(AC) = (CD)/(CB) = (1)/(2)`

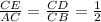
iv) Angle ACB or ∠C is common to Δ ACB and Δ CED.

v) Therefore from the above 4 equations we can say that by

SAS theorem the two triangles are similar , that is , Δ ECD
`\sim` Δ ACB .

Therefore option A is Correct.

vi) Yes it can be proven that ED || AB after proving that Δ ECD
`\sim` Δ ACB.

Since Δ ECD
`\sim` Δ ACB , therefore ∠CED = ∠CAB and ∠CDE = ∠CBA.

Therefore we can say that ED is parallel to AB or that ED || AB.