Answer:
|SQ|=5
Explanation:
If S is the median, then OP is a median of triangle OMN.
This implies that:
|MP|=|NP|
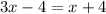
We group like terms and solve for x.
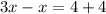
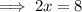
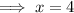
Now we know that: MN:SQ=2:1
But MN=2x+2
This implies that:
2x+2:SQ=2:1
Put x=4
2(4)+2:SQ=2:1
10:SQ=2:1
Therefore |SQ|=5