Question

As a first step in solving the system shown, Yumiko multiplies both sides of the equation 2x – 3y = 12 by 6. By what factor should she multiply both sides of the other equation so that she can add the equations and eliminate a variable? What one-variable equation is she left with after adding?

5x + 6y = 18
2x – 3y = 12

Factor:________
Equation:________x=_________

Answer 1

Yumiko should multiply the other equation by 3.

If she adds the two equations she would be left with the variable 'x'.

Explanation:

Given the two equations are as follows:

`$ 2x - 3y = 12 \hspace{5mm} \hdots (1) $`

`$ 5x + 6y = 18 \hspace{5mm} \hdots (2) $`

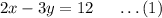
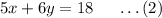
It is given that she multiplies the first equation by 6. Therefore, (1) becomes

`$ 12x - 18y = 72 \hspace{15mm} \hdots (a) $`

Now, note that the sign of the variable 'y' is negative. So, if we make the co-effecient of 'y' equal in both the cases, add them it would result in the elimination of the variable 'y'.

The co-effecient of y in Equation (2) is 6. To make it 18 like it is in Equation (1), we multiply throughout by 3.

Therefore, Equation (2) becomes:

`$ 15x + 18y = 54 \hspace{5mm} \hdots (b) $`

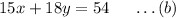
Now, we add Equation (a) and Equation (b).

`$ \implies 12x - 18y + 15x + 18y = 72 + 54 $`

`$ \implies 27x = 126 $`

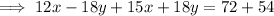
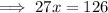
Factor: 3

Equation: 27x = 126