Answer:
- Rounding to nearest tenth of centimeter, the ball bounces 192.1 cm high on the 5th bounce.
Step-by-step explanation:
The ball is dropped from a height of 900 centimeters.
Since the heights form a geometric sequence, you can find a common ratio between consecutive terms. This is:
- Height bounce 2 / height bounce 1 = 560 / 800 = 0.7
- Height bound 3 / height bounce 2 = 392 / 560 = 0.7
Hence, the ratio of the geometric sequence is 0.7, and taking bounce 1 as the start of the sequence, the general term of the sequence is:
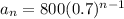
With that formula you can find any term:
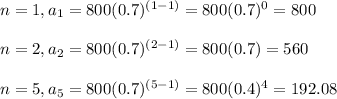
Rounding to nearest tenth of centimeter, the ball bounces 192.1 cm high on the 5th bounce.