Question

g If there are 52 cards in a deck with four suits (hearts, clubs, diamonds, and spades), how many ways can you select 5 diamonds and 3 clubs?

Answer 1

The number of ways to select 5 diamonds and 3 clubs is 368,082.

Explanation:

In a standard deck of 52 cards there are 4 suits each consisting of 13 cards.

Compute the probability of selecting 5 diamonds and 3 clubs as follows:

The number of ways of selecting 0 cards from 13 hearts is:

`{13\choose 0}=(13!)/(0!*(13-0)!) =(13!)/(13!)=1`

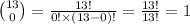
The number of ways of selecting 3 cards from 13 clubs is:

`{13\choose 3}=(13!)/(3!*(13-3)!) =(13!)/(13!*10!)=286`

The number of ways of selecting 5 cards from 13 diamonds is:

`{13\choose 5}=(13!)/(5!*(13-5)!) =(13!)/(13!*8!)=1287`

The number of ways of selecting 0 cards from 13 spades is:

`{13\choose 0}=(13!)/(0!*(13-0)!) =(13!)/(13!)=1`

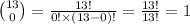
Compute the number of ways to select 5 diamonds and 3 clubs as:

`{13\choose0}*{13\choose3}*{13\choose5}*{13\choose0} = 1*286*1287*1=368082`

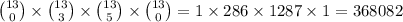
Thus, the number of ways to select 5 diamonds and 3 clubs is 368,082.