Question

Suppose you choose a team of two people from a group of n > 1 people, and your opponent does the same (your choices are allowed to overlap). Show that the number of possible choices of your team and the opponent’s team equals Pn−1 i=1 i 3 .

Answer 1

The number of possible choices of my team and the opponents team is

`\left\begin{array}{ccc}n-1\\E\\n=1\end{array}\right i^(3)`

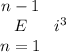
Explanation:

selecting the first team from n people we have
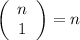`\left(\begin{array}{ccc}n\\1\\\end{array}\right) = n` possibility and choosing second team from the rest of n-1 people we have
`\left(\begin{array}{ccc}n-1\\1\\\end{array}\right) = n-1`

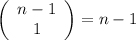
As { A, B} = {B , A}

Therefore, the total possibility is
`(n(n-1))/(2)`

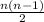
Since our choices are allowed to overlap, the second team is
`(n(n-1))/(2)`

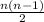
Possibility of choosing both teams will be

`(n(n-1))/(2) * (n(n-1))/(2) \\\\= [(n(n-1))/(2)] ^(2)`

We now have the formula

1³ + 2³ + ........... + n³ =
`[(n(n+1))/(2)] ^(2)`

1³ + 2³ + ............ + (n-1)³ =
`[x^(2) (n(n-1))/(2)] ^(2)`

=
`\left[\begin{array}{ccc}n-1\\E\\i=1\end{array}\right] = [(n(n-1))/(2)]^(3)`