Answer:
Yes it is a function given by f(x) = 2x
Explanation:
Any function can approximated as series or a polynomial. For example,
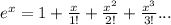 (exponential function)
(exponential function)
(n! or n factorial is equal to n(n-1)(n-2)...3.2.1 ; 3! = 3.2.1 = 6)
and for the series to converge(the sum does not go to infinity), higher order terms must tend to zero.
General form of a polynomial/series:
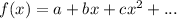
For the given set of points, we can start with the straight line equation:
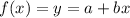 ........(1)
........(1)
Let us take two points from the given relation: (-5, -10), (-1, -2)
and put the respective x and y values in equation (1), we get two equations, which we can then solve simultaneously to get values of
 and
and
 :
:
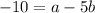 ........(2)
........(2)
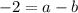 ..........(3)
..........(3)
Now (3) - (2) gives us:
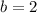 and putting the value of
and putting the value of
 in any of the above equation gives us
in any of the above equation gives us
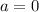
Hence, we get the equation,
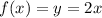
It can be seen that all the given points satisfies this relation and since we get a unique
 for every
for every
 , we can call this a function.
, we can call this a function.