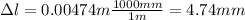Answer: 4.74 mm
Step-by-step explanation:
We can solve this problem with the following equation:
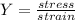 (1)
(1)
Where:
 is the Young modulus for femur
is the Young modulus for femur
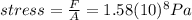 is the stress (force
is the stress (force
 applied per unit of transversal area
applied per unit of transversal area
 ) on the femur
) on the femur
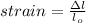
Being:
 the compression the femur can withstand before breaking
the compression the femur can withstand before breaking
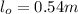 is the length of the femur without compression
is the length of the femur without compression
Writing the data in equation (1):
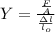 (2)
(2)
 (3)
(3)
Isolating
 :
:
 (4)
(4)
 (5) This is the compression in meters
(5) This is the compression in meters
Converting this result to millimeters: