Question

Calculate the speed of an electron (in m/s) after it accelerates from rest through a potential difference of 160 V.

Answer 1

v = 7.5*10⁶ m/s

Step-by-step explanation:

While accelerating through a potential difference of 160 V, the electron undergoes a change in the electric potential energy, as follows:

ΔUe = q*ΔV = (-e)*ΔV = (-1.6*10⁻¹⁹ C) * 160 V = -2.56*10⁻¹⁷ J (1)

Due to the principle of conservation of energy, in absence of non-conservative forces, this change in potential energy must be equal to the change in kinetic energy, ΔK:

ΔK = Kf -K₀

As the electron accelerates from rest, K₀ =0.

⇒ΔK =Kf =
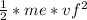`(1)/(2)*me*vf^(2)` (2)

From (1) and (2):

ΔK = -ΔUe = 2.56*10⁻¹⁷ J =
`(1)/(2)*me*vf^(2)`

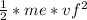
where me = mass of the electron = 9.1*10⁻³¹ kg.

Solving for vf:

`vf =\sqrt{(2*(2.56e-17J))/(9.1e-31kg) } =7.5e6 m/s`

⇒ vf = 7.5*10⁶ m/s