Question

A disk of radius 2.0 cm has a surface charge density of 6.3 μC/m2 on its upper face. What is the magnitude of the electric field produced by the disk at a point on its central axis at distance z = 12 cm from the disk?

Answer 1

the electric field at Z = 12 cm is E = 9.68 × 10³ N/C = 9.68 kN/C

Step-by-step explanation:

Given: radius of disk, R = 2.0 cm = 2 × 10⁻² cm, surface charge density,σ = 6.3 μC/m² = 6.3 × 10⁻⁶ C/m², distance on central axis, z = 12 cm = 12 × 10⁻² cm.

The electric field, E at a point on the central axis of a charged disk is given by E = σ/ε₀(
`1 - \frac{z}{\sqrt{z^(2) + R^(2) } }`)

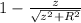Substituting the values into the equation, it becomes

E = σ/ε₀(
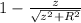`1 - \frac{z}{\sqrt{z^(2) + R^(2) } }`) = 6.3 × 10⁻⁶/8.854 × 10⁻¹²(
`1 - \frac{0.12}{\sqrt{0.12^(2) + 0.02^(2) } }`) = 7.12 × 10⁵(
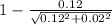`1 - (0.12)/(0.1216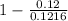)`) = 7.12 × 10⁵(1 - 0.9864) = 7.12 × 10⁵ × 0.0136 = 0.0968 × 10⁵ = 9.68 × 10³ N/C = 9.68 kN/C

Therefore, the electric field at Z = 12 cm is E = 9.68 × 10³ N/C = 9.68 kN/C