x ≤ 12
Solution:
Let us take the number be x.
A number : x
A number divided by three :
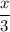
A number divided by three less two :
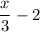
A number divided by three less two is at most two :
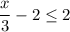
Now, simplify the inequality,
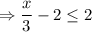
Add 2 on both sides of the inequality,

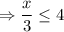
Multiply by 3 on both sides of the equation,
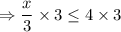
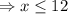
Hence x ≤ 12.