Question

Calculate the fraction of atoms in a sample of argon gas at 400 K that have an energy of 10.0 kJ or greater.

Answer 1

The answer to this can be arrived at by clculating the mole fraction of atoms higher than the activation energy of 10.0 kJ by pluging in the values given into the Arrhenius equation. The answer to this is 20.22 moles of Argon have energy equal to or greater than 10.0 kJ

Step-by-step explanation:

From Arrhenius equation showing the temperature dependence of reaction rates.

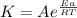`K = Ae^{(Ea)/(RT) }` where

k = rate constant

A = Frequency or pre-exponential factor

Ea = energy of activation

R = The universal gas constant

T = Kelvin absolute temperature

we have

`f = e^{(Ea)/(RT) }`

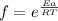
Where

f = fraction of collision with energy higher than the activation energy

Ea = activation energy = 10.0kJ = 10000J

R = universal gas constant = 8.31 J/mol.K

T = Absolute temperature in Kelvin = 400K

In the Arrhenius equation k = Ae^(-Ea/RT), the factor A is the frequency factor and the component e^(-Ea/RT) is the portion of possible collisions with high enough energy for a reaction to occur at the a specified temperature

Plugging in the values into the equation relating f to activation energy we get

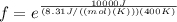`f = e^{(10000J)/((8.31J/((mol)(K)))(400K)) }` or f =
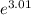`e^(3.01)` = 20.22 moles of argon have an energy of 10.0 kJ or greater