Question

Determine the magnitude of the acceleration experienced by an electron in an electric field of 664 N/CN/C .

Answer 1

`a=-1.17* 10^(14) \hspace{3}(m)/(s^2)`

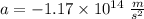
Step-by-step explanation:

A charged particle that is in a region where there is an electric field, experiences a force equal to the product of its charge by the intensity of the electric field:

`F_e=q*E`

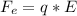
If the electric field is uniform, the force is constant and so is the acceleration. Applying the equations of uniformly accelerated rectilinear motion, we obtain the velocity of the particle at any time or after having moved a certain distance:

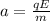`a=(qE)/(m)` (1)

Where:

`E=Electric\hspace{3}field\hspace{3}strength=664(N)/(C) \\q=Electric\hspace{3}charge\hspace{3}of\hspace{3}the\hspace{3}particle\\m=Mass\hspace{3}of\hspace{3}the\hspace{3}particle`

The electric charge and the mass of the electron are known constants:

`q=-1.6* 10^(-19) C\\m=9.1* 10^(-31) kg`

So, replacing this data in the equation (1) :

`a=((-1.6* 10^(-19))*(664) )/(9.1* 10^(-31) ) =-1.167472527* 10^(14) \approx -1.17* 10^(14) \hspace{3}(m)/(s^2)`

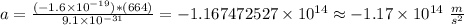
The minus sign is due to the fact that the charge is negative, therefore it experiences a force in the opposite direction to the field.