Question

At a used dealership, let X be an independent variable representing the age in years of a motorcycle and Y be the dependent variable representing the selling price of used motorcycle. The data is now given to you.

X = {5, 10; 12, 14, 15}; Y = {500, 400, 300, 200, 100}

(a) Write the regression model.
(b) Estimate the parameters of the model
(c) Write the prediction equation
(d) Calculate SSE.

Answer 1

a) Selling price y= a + b (age x)

b)

a= 728.025

b= -38.217

c)

Selling price y = 728.025 - 38.217 age x

d)

SSE=8280.25

Explanation:

a)

The regression model can be written as

y=a+bx

Here y=selling price and x is age.

So, the regression model will be

Selling price y= a + b (age x)

b)

We have to find the values of "a" and "b"

`b=(nsumxy-(sumx)(sumy))/(nsumx^(2) -(sumx)^2)`

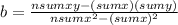
sumx=5+10+12+14+15=56

sumy=500+400+300+200+100=1500

sumxy=5*500+10*400+12*300+14*200+15*100=14400

sumx²=5²+10²+12²+14²+15²=690

n=5

`b=(5(14400)-(56)(1500))/(5(690) -(56)^2)`

b=-12000/314

b=-38.217

ybar=a+bxbar

a=ybar-bxbar

ybar=sumy/n=1500/5=300

xbar=sumx/n=56/5=11.2

a=300-(-38.217)(11.2)

a=300+428.025

a=728.025

c)

Selling price y = a - b(age x)

Selling price y = 728.025 - 38.217 age x

d)

SSE known as sum of square of error can be calculated as

SSE=sum(y-yhat)²

y 500 400 300 200 100

x 5 10 12 14 15

yhat= 728.025 - 38.217 age x 536.940 345.855 269.421 192.987 154.770

y-yhat -36.940 54.145 30.579 7.013 -54.770

(y-yhat)² 1364.56 2931.68 935.08 49.18 2999.75

SSE=sum(y-yhat)²

SSE=1364.56 +2931.68 +935.08 +49.18 +2999.75

SSE =8280.25