Question

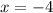
Name 3 of the 4 features listed below for the function g (x) = log2 (x + 4) - 1 and include a description of how you found those answers using complete sentences. 1) Vertical Asymptote 2) Domain 3) X and Y Intercepts 4) Transformations compared to its parent function f (x) = log2 x

Answer 1

(1) Vertical asymptote:
`x=-4`

(2) Domain:
`x>-4`

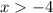
(3) X intercept:
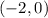`(-2,0)` and Y intercept :
`(0,1)`

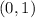
(4) The function g(x) is shifted 4 units to the left and shifted 1 unit down.

Step-by-step explanation:

The parent function is
`f(x)=\log _(2) x`

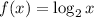
The transformed function is
`g(x)=\log _(2)(x+4)-1`

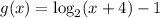
(1) Vertical asymptote:

The vertical asymptote of a function can be determined by equating

`x+4=0`

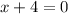
Thus,
`x=-4`

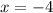
The vertical asymptote is
`x=-4`

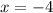
(2) Domain:

The domain of a function is the set of all independent x-values.

`x+4>0`

Thus,
`x>-4`

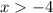
The domain of a function is
`x>-4`

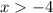
(3) X and Y intercepts:

To determine the x intercept, let us substitute y=0 in
`g(x)=\log _(2)(x+4)-1`

`\begin{equation}\begin{aligned}\log _(2)(x+4)-1 &=0 \\\log _(2)(x+4) &=1 \\x+4 &=2^(1) \\x &=-2\end{aligned}`

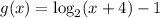
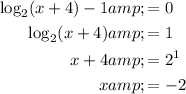
Thus, the x intercept is
`(-2,0)`

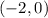
To determine the y intercept, let us substitute x=0 in
`g(x)=\log _(2)(x+4)-1`

`\begin{equation}\begin{aligned}y &=\log _(2)(0+4)-1 \\&=\log _(2) 4-1 \\&=2-1 \\&=1\end{aligned}`

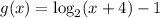
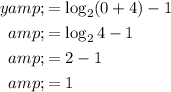
Thus, the y intercept is
`(0,1)`

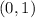
(4) To determine the transformation:

The transformed function
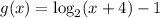`g(x)=\log _(2)(x+4)-1` is shifted 4 units to the left and shifted 1 unit downwards.