Question

Determine the point of discontinuity if it exists
v(x)=x^2-25/2x^2+13x+15

Answer 1

x=-5 and x=-1.5

Explanation:

The given function is

`v(x) = \frac{{x}^(2) - 25}{2 {x}^(2) + 13x + 15}`

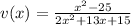
The points of discontinuity occurs at where the denominator is zero.

`2 {x}^(2) + 13x + 15= 0`

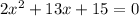
We solve by factoring.

We first split the middle term:

`2 {x}^(2) + 3x + 10x + 15= 0`

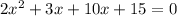
We factor by grouping:

`x(2x + 3) + 5(2x + 3)= 0`

`(x + 5)(2x + 3) = 0`

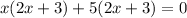
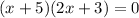
The points of discontinuity occur at x=-5, and x=-1.5