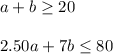Question

Jonah is going to the store to buy candles. Small candles cost $2.50 and large candles cost $7.00. He needs to buy at least 20 candles, and he can spend no more than 80 dollars. Make this into a system of linear inequalities to model each situation. DEFINE YOUR VARIABLES! (No Solving is required, just equation.)

Answer 1

The system of linear inequalities are:

`a + b \geq 20\\\\2.50a + 7b\leq 80`

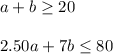
Solution:

Let "a" be the number of small candles bought

Let "b" be the number of large candles bought

Cost of each small candle = $ 2.50

Cost of each large candle = $ 7

He needs to buy at least 20 candles

Therefore, number of small candles and number of large candles bought must be at least 20

Thus, we frame a inequality as:

`a + b\geq 20`

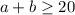
"at least" means greater than or equal to

Here, we used "greater or equal to" symbol because, he can buy 20 candles or more than 20 candles also

He can spend no more than 80 dollars

Which means, he spend maximum 80 dollars or less than 80 dollars also

So we have to use "less than or equal to" symbol

Thus, we frame a inequality as:

Number of small candles bought x Cost of 1 small candle + number of large candles bought x Cost of 1 large candle
`\leq` 80

`a * 2.50 + b * 7 \leq 80\\\\2.50a + 7b\leq 80`

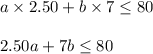
Thus the system of linear inequalities are:

`a + b \geq 20\\\\2.50a + 7b\leq 80`