Question

A 5.67 gram coin is placed on a record that is rotating at 33.3 rpm. If the coefficient of the static friction is 0.100, how far from the center of the record can the coin be placed without having it slip off?

Answer 1

81 mm from the center

Step-by-step explanation:

5.67g = 0.00567 kg

33.3 revolutions per minute = 33.3 (rev/min) * 2π (rad/rev) * (1/60) (min/sec) = 3.487 rad/s

The weight of the coin is product of mass and gravitational acceleration g = 9.81m/s2

W = mg = 0.00567 * 9.81 = 0.0556 N

Which is also the normal force of the record acting back on the coin to balance it.

Them the static friction is product of normal force and friction coefficient

`F_f = N\mu = 0.0556*0.1 = 0.00556 N`

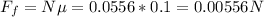
For the coin to NOT slip off, its centripetal force should at most be equal to the static friction

`F_c = 0.00556`

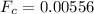
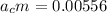`a_cm = 0.00556` Newton's 2nd law

`a_c = 0.00556 / 0.00567 = 0.981 m/s^2`

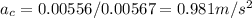
The centripetal acceleration is the product of squared angular velocity and radius of circular motion

`a_c = \omega^2r`

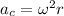
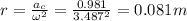`r = (a_c)/(\omega^2) = (0.981)/(3.487^2) = 0.081m` or 81 mm