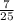Question

Given tan A =7/24, find the sin B and tan b. A. 7/25 B. 24/7 C. 24/25 D. 7/24

Answer 1

Question:

Given tan B =7/24, find the sin B

Answer:

Option A

`sin\ B = (7)/(25)`

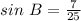
Solution:

Given that,

`tan\ B = (7)/(24)`

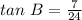
We have to find sin B

We know that by trignometric ratios,

`tan = (opposite)/(adjacent)`

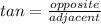
From given,

`tan\ B = (7)/(24)`

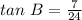
On comparing we get,

Opposite = 7

Adjacent = 24

We can find the hypotenuse

`hypotenuse^2 = opposite^2 + adjacent^2\\\\hypotenuse^2 = 7^2 + 24^2\\\\hypotenuse^2 = 49 + 576\\\\hypotenuse^2 = 625\\\\Take\ square\ root\ on\ both\ sides\\\\hypotenuse = 25`

Thus Sin B is given as:

`sin\ B = (opposite)/(hypotenuse)\\\\sin\ B = (7)/(25)`

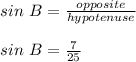
Thus, sin B is
`(7)/(25)`