Question

Problem 4 A meteoroid is first observed approaching the earth when it is 402,000 km from the center of the earth with a true anomaly of 150 deg. If the speed of the meteoroid at that time is 2.23 km/s, calculate: (a) the eccentricity of the trajectory, (b) the altitude at closest approach, (c) the speed at the closest approach, (d) the aiming radius and turn angle, and (e) the C3 of the meteoroid. Sketch the orbit.

Answer 1

Part a: The eccentricity is 1.086.

Part b: The altitude at closest approach is 5088 km

Part c: The velocity at perigee is 8.516 km/s

Part d: The turn angle is 134.08 while the aiming radius is 5641.28 km

Step-by-step explanation:

Part a

Specific energy is given by

`\epsilon=(v^2)/(2)-(\mu)/(r)`

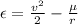
Here

• ε is the specific energy
• v is the velocity which is given as 2.23 km/s
• μ is the gravitational constant whose value is 398600
• r is the distance between earth and the meteorite which is 402,000 km

`\epsilon=(v^2)/(2)-(\mu)/(r)\\\epsilon=(2.2^2)/(2)-(398600)/(402,000)\\\epsilon=1.495 km^2/s^2`

Value of specific energy is also given as

`\epsilon=(\mu)/(2a)\\a=(\mu)/(2\epsilon)\\a=(398600)/(2* 1.495)\\a=13319 km`

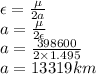
Orbit formula is given as

`r=a((e^2-1)/(1+ecos \theta))\\ae^2-recos\theta-(a+r)=0`

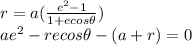
Putting values in this equation and solving for e via the quadratic formula gives

`ae^2-recos\theta-(a+r)=0\\(133319)e^2-(402000)(cos 150) e-(133319+402000)=0\\133319e^2+348142.21 e-535319=0\\\\e=(-348142.21 \pm √(348142.21^2-4(133319)(535319)))/(2 (133319))\\\\e=1.086 \, or \, -3.69`

As the value of eccentricity cannot be negative so the eccentricity is 1.086.

Part b

The radius of trajectory at perigee is given as

`r_p=a(e-1)\\`

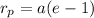
Substituting values gives

`r_p=133319 (1.086-1)\\r_p=11465.4 km`

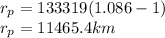
Now for estimation of altitude z above earth is given as

`z=r_p-R_E\\z=11465.4-6378\\z=5087.434\\z\approx 5088 km`

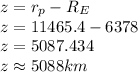
So the altitude at closest approach is 5088 km

Part c

radius of perigee is also given as

`r_p=(h^2)/(\mu)(1)/(1+e)`

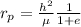
Rearranging this equation gives

`h=√(r_p\mu(1+e))\\h=√(11465.4 * 3986000 * (1+1.086))\\h=97638.489 km^2/s`

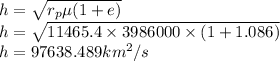
Now the velocity at perigee is given as

`v_p=(h)/(r_p)\\v_p=(97638.489)/(11465.4)\\v_p=8.516 km/s\\`

So the velocity at perigee is 8.516 km/s

Part d

Turn angle is given as

`\delta =2 sin^(-1) ((1)/(e))`

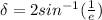
Substituting value in the equation gives

`\delta =2 sin^(-1) ((1)/(e))\\\delta =2 sin^(-1) ((1)/(1.086))\\\delta =134.08`

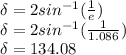
Aiming radius is given as

`\Delta =a √(e^2-1)`

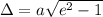
Substituting value in the equation gives

`\Delta =a √(e^2-1)\\\Delta =13319 √(1.086^2-1)\\\Delta=5641.28 km`

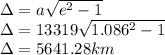
So the turn angle is 134.08 while the aiming radius is 5641.28 km