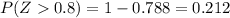Question

If the filling equipment is functioning properly what is the probability that the volume of oil in a randomly selected barrel will be 55.4 gallons or more? Show your work?

Answer 1

`P(X>55.4)=P((X-\mu)/(\sigma)>(55.4-\mu)/(\sigma))=P(Z>(55.4-55)/(0.5))=P(Z>0.8)`

`P(Z>0.8)=1-P(Z\leq 0.8)`

`P(Z>0.8)=1-0.788=0.212`

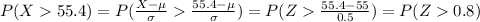
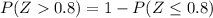
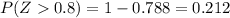
Explanation:

Assuming this previous info : "Trucks carry barrels of crude oil from a port in Texas to a distributer in New Mexico on long trailers. Filling equipment is used to fill the barrels with the oil. When functioning properly, the actual volume of oil loaded into each barrel by the filling equipment at the port is approximately normally distributed with a mean of 55 gallons and a standard deviation of 0.5 gallons. If the mean is greater than 55.4 gallons, the filling mechanism is overfilling."

Previous concepts

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".

Solution to the problem

Let X the random variable that represent the amount filling of a population, and for this case we know the distribution for X is given by:

`X \sim N(55,0.5)`

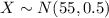
Where
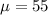`\mu=55` and
`\sigma=0.5`

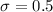
We are interested on this probability

`P(X>55.4)`

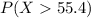
And the best way to solve this problem is using the normal standard distribution and the z score given by:

`z=(x-\mu)/(\sigma)`

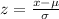
If we apply this formula to our probability we got this:

`P(X>55.4)=P((X-\mu)/(\sigma)>(55.4-\mu)/(\sigma))=P(Z>(55.4-55)/(0.5))=P(Z>0.8)`

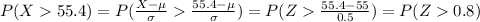
And we can find this probability using the complement rule:

`P(Z>0.8)=1-P(Z\leq 0.8)`

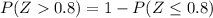
And in order to find these probabilities we can use tables for the normal standard distribution, excel or a calculator.

`P(Z>0.8)=1-0.788=0.212`