Question

A tree casts a 12 foot shadow while the sun is at an angle of elevation of 58º. Use

this information to approximate the height of the tree to the nearest tenth of a foot.

Answer 1

The height of tree is 32 meter

Solution:

Given that, The sun is at an angle of elevation of 58 degree

A tree casts a shadow 20 meters long on the ground

The sun, tree and shadow forms a right angled triangle

The figure is attached below

ABC is a right angled triangle

AC is the height of tree

AB is the length of shadow

AB = 20 meters

Angle of elevation, angle B = 58 degree

By definition of tan,

`tan \theta = (opposite)/(adjacent)`

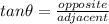
In this right angled triangle ABC,

opposite = AC and adjacent = AB

Therefore,

`tan\ 58 = (AC)/(AB)\\\\tan\ 58 = (AC)/(20)\\\\1.6 = (AC)/(20)\\\\AC = 1.6 * 20\\\\AC = 32`

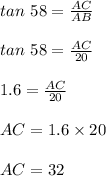
Thus height of tree is 32 meter