Question

BONUS: Name the restrictions, solve, & SHOW your check.
x + 1 = √(5x+11)

Answer 1

x = 5

Solution:

Given equation is
`x+1=√(5x+11)`.

`\Rightarrow x+1=√(5x+11)`

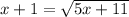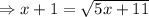
Squaring on both sides of the equation to remove the square root.

`\Rightarrow (x+1)^2=(√(5x+11))^2`

`\Rightarrow (x+1)^2=5x+11`

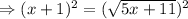
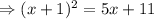
Using algebraic identity:
`(a+b)^2=a^2+2ab+b^2`

`\Rightarrow x^2+2x(1)+1^2=5x+11`

`\Rightarrow x^2+2x+1=5x+11`

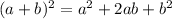
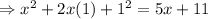
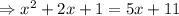
Combine all terms in one side of the equation.

`\Rightarrow x^2+2x+1-5x-11=0`

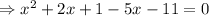
Arrange like terms together.

`\Rightarrow x^2+2x-5x+1-11=0`

`\Rightarrow x^2-3x-10=0`

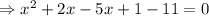
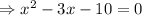
Now solve by factorization.

`\Rightarrow x^2-5x+2x-10=0`

`\Rightarrow (x^2-5x)+(2x-10)=0`

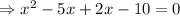
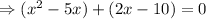
Take common terms on left side of the term.

`\Rightarrow x(x-5)+2(x-5)=0`

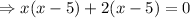
Now, take (x – 5) common on both terms.

`\Rightarrow (x+2)(x-5)=0`

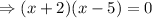
⇒ x + 2 = 0 (or) x – 5 = 0

⇒ x = –2 (or) x = 5

If we put x = –2 in the given equation,

`-2+1=√(5(-2)+11)`

`\Rightarrow-1=1`

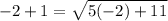
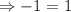
It is false. So, x = –2 is not true.

If we put x = 5 in the given equation,

`5+1=√(5*5+11)`

`5+1=√(36)`

`\Rightarrow6=6`

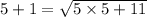
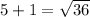
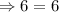
It is true. So, x = 5 is true.

Hence x = 5 is the solution.