Question

A bag contains 6 gray tiles and 3 blue tiles. Jenny reached into the bag and picked a tile

randomly, and then without replacing it, picked a second tile.

What is the probability that she
picked a gray tile with her second pick given that she picked a blue tile with her first pick?​

Answer 1

The probability that Jenny picked a gray tile with her second pick given that she picked a blue tile with her first pick = 0.25

Explanation:

i.) there are 6 gray tiles and 3 blue tiles

ii) the probability that Jenny picked a blue tile first is given by

`\frac{number\hspace{0.1cm} of \hspace{0.1cm} blue\hspace{0.1cm} tiles }{total \hspace{0.1cm}number\hspace{0.1cm} of \hspace{0.1cm}tiles\hspace{0.1cm} } = (3)/(9) = (1)/(3)`

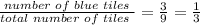
iii) the probability that Jenny picked a gray tile with her second pick without replacing the first tile
`\frac{number\hspace{0.1cm} of \hspace{0.1cm} blue\hspace{0.1cm} tiles }{total \hspace{0.1cm}number\hspace{0.1cm} of \hspace{0.1cm}tiles\hspace{0.1cm} } * \frac{number\hspace{0.1cm} of \hspace{0.1cm} gray\hspace{0.1cm} tiles }{total \hspace{0.1cm}number\hspace{0.1cm } of \hspace{0.1cm}tiles\hspace{0.1cm} - 1 } = (3)/(9) * (6)/(8) = (1)/(3) * (3)/(4) = (1)/(4) = 0.25`

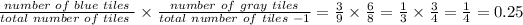
The probability that Jenny picked a gray tile with her second pick given that she picked a blue tile with her first pick = 0.25