Answer:
please see answers are as in the explanation.
Explanation:
As from the data of complete question,
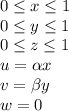
The question also has 3 parts given as
Part a: Sketch the deformed shape for α=0.03, β=-0.01 .
Solution
As w is 0 so the deflection is only in the x and y plane and thus can be sketched in xy plane.
the new points are calculated as follows
Point A(x=0,y=0)
Point A'(x+αx,y+βy)
Point A'(0+(0.03)(0),0+(-0.01)(0))
Point A'(0,0)
Point B(x=1,y=0)
Point B'(x+αx,y+βy)
Point B'(1+(0.03)(1),0+(-0.01)(0))
Point B'(1.03,0)
Point C(x=1,y=1)
Point C'(x+αx,y+βy)
Point C'(1+(0.03)(1),1+(-0.01)(1))
Point C'(1.03,0.99)
Point D(x=0,y=1)
Point D'(x+αx,y+βy)
Point D'(0+(0.03)(0),1+(-0.01)(1))
Point D'(0,0.99)
So the new points are A'(0,0), B'(1.03,0), C'(1.03,0.99) and D'(0,0.99)
The plot is attached with the solution.
Part b: Calculate the six strain components.
Solution
Normal Strain Components
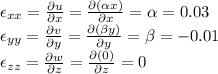
Shear Strain Components
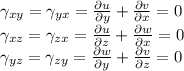
Part c: Find the volume change
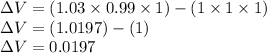
Also the change in volume is 0.0197
For the unit cube, the change in terms of strains is given as
![\Delta V={V_0}[(1+\epsilon_(xx))]*[(1+\epsilon_(yy))]* [(1+\epsilon_(zz))]-[1 * 1 * 1]\\\Delta V={V_0}[1+\epsilon_(xx)+\epsilon_(yy)+\epsilon_(zz)+\epsilon_(xx)\epsilon_(yy)+\epsilon_(xx)\epsilon_(zz)+\epsilon_(yy)\epsilon_(zz)+\epsilon_(xx)\epsilon_(yy)\epsilon_(zz)-1]\\\Delta V={V_0}[\epsilon_(xx)+\epsilon_(yy)+\epsilon_(zz)]\\](https://img.qammunity.org/2021/formulas/mathematics/college/kbse41acclb7w93o5rylw3vu5k09khj8ib.png)
As the strain values are small second and higher order values are ignored so
![\Delta V\approx {V_0}[\epsilon_(xx)+\epsilon_(yy)+\epsilon_(zz)]\\ \Delta V\approx [\epsilon_(xx)+\epsilon_(yy)+\epsilon_(zz)]\\](https://img.qammunity.org/2021/formulas/mathematics/college/k4f08h4qtqb9yc760ob3ttj3bb4yceazly.png)
As the initial volume of cube is unitary so this result can be proved.