Question

A 200 kg weather rocket is loaded with 100 kg of fuel and fired straight up. It accelerates upward at 35 m/s2 for 35 s , then runs out of fuel. Ignore any air resistance effects. How long is the rocket in the air before hitting the ground?

Answer 1

T = 295.57 s

Step-by-step explanation:

given,

mass of the rocket = 200 Kg

mass of the fuel = 100 Kg

acceleration = 35 m/s²

time, t = 35 s

time taken by the rocket to hit the ground, = ?

Final speed of the rocket when fuel is empty

using equation of motion

v = u + a t

v = 0 + 35 x 35

v = 1225 m/s

height of the rocket where fuel is empty

v² = u² + 2 a s

1225² = 0 + 2 x 35 x h₁

h₁ = 21437.5 m

After 35 s the rocket will be moving upward till the final velocity becomes zero.

Now, using equation of motion to find the height after 35 s

v² = u² + 2 g h₂

0² = 1225² + 2 x (-9.8) h₂

h₂ = 76562.5 m

total height = h₁ + h₂

= 76562.5 m + 21437.5 m = 98000 m

now, time taken by before the rocket hit the ground

using equation of motion

`s = u t +(1)/(2)at^2`

`-13500 = 1225 t -(1)/(2)* 9.8 * t^2`

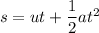
negative sign is used because the distance travel by the rocket is downward.

4.9 t² - 1225 t - 13500 = 0

`t = (-(-1225)\pm √(1225^2 - 4* 4.9 * (-13500)))/(2* 4.9)`

t = 260.57 s

neglecting the negative sign

total time the rocket was in air

T = t₁ + t₂

T = 35 + 260.57

T = 295.57 s

Time for which rocket was in air is equal to 295.57 s.