Question

The vector w=ai+bj is perpendicular to the line ax+by=c and parallel to the line bx−ay=c. It is also true that the acute angle between intersecting lines that do not cross at right angles is the same as the angle determined by vectors that are either normal to the lines or parallel to the lines. Use this information to find the acute angle between the lines below. yx+9y=0​, −4x+5y=3

Answer 1

Answer with Step-by-step explanation:

We are given that

`yx+9y=0`

`-4x+5y=3`

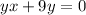
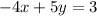
We have to find the angle between the lines.

`y(x+9)=0`

`y=0,x+9=0\implies x=-9`

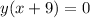
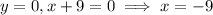
`y=0`..(1)

`x=-9`..(2)

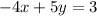`-4x+5y=3`..(3)

The angle between two lines

`a_1x+b_1y+c_1=0`

`a_2x+b_2y+c_2=0`

`tan\theta=\mid (a_1b_2-b_1a_2)/(a_1a_2+b_1b_2)\mid`

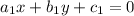
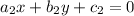
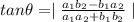
By using the formula the angle between equation (1) and equation (2) is given by

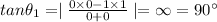`tan\theta_1=\mid(0* 0-1* 1)/(0+0)\mid=\infty=90^(\circ)`degree

`tan90^(\circ)=\infty`

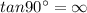
It is not possible because we are given that the acute angle between intersecting lines that do not cross at right angles is same as the angle determined by vectors that either normal to the lines or parallel to lines.

By using the formula the angle between equation (2) and equation(3)

`tan\theta_2=\mid(1(5)-0(4))/(-4(1)+5(0))\mid=(5)/(4)`

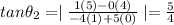
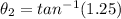`\theta_2=tan^(-1)(1.25)` degree

By using the formula the angle between equation (3) and equation(1)

`tan\theta_3=\mid(-4(1)-5(0))/(-4(0)+5(1))\mid=(4)/(5)`

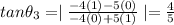
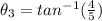`\theta_3=tan^(-1)((4)/(5))`degree