Question

A dead body was found within a closed room of a house where the temperature was a constant 65° F. At the time of discovery the core temperature of the body was determined to be 85° F. One hour later a second measurement showed that the core temperature of the body was 80° F. Assume that the time of death corresponds to t = 0 and that the core temperature at that time was 98.6° F. Determine how many hours elapsed before the body was found.

Answer 1

1 hr 52 minutes

Explanation:

As per Newton law of cooling we have

`T(t) = T_s +(T_0-T_s)e^(-kt)`

where T0 is the initial temperature of the body

Ts = temperature of surrounding

t = time lapsed

k = constant

Using this we find that T0 = 98.6 : Ts= 65

Let x hours be lapsed before the body was found.

Then we have

`T(x) = 65 +(98.6-65)e^(-kx) = 85\\e^(-kx)=(20)/(33.8) =0.5917`

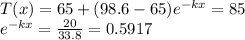
Next after 1 hour temperature was 80

`T(x+1) = 65+33.6(e^(-k(x+1))=80\\e^{-k(x+1) =0.4464`

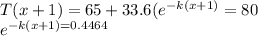
Dividing we get

`e^k = 1.325408\\k = 0.2817`

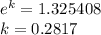
Substitute this in

`e^(-kx) =0.5917\\x=(ln 0.5917)/(-k) \\=1.863`

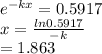
approximately 1 hour 52 minutes have lapsed.