Question

Suzie invests $500 in an account that is compounded continuously at an annual interest rate of 5%, according to the formula A=Pe^rt, where A is the amount accrued, P is the principle, r is the rate of interest, and t is the time, in years. Approximately how many years will it take for Suzie's money to double?

a. 1.4
b. 6.0
c. 13.9
d. 14.7

Answer 1

c. 13.9

Explanation:

We have been given that Suzie invests $500 in an account that is compounded continuously at an annual interest rate of 5%. We are asked to find the time it will take for Suzie's money to double.

We will use continuous compounding interest formula to solve our given problem.

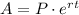`A=P\cdot e^(rt)`, where A is the amount accrued, P is the principle, r is the rate of interest, and t is the time, in years.

`5\%=(5)/(100)=0.05`

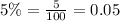
Double of $500 would be $1000.

`1000=500\cdot e^(0.05t)`

`(1000)/(500)=(500\cdot e^(0.05t))/(500)`

`2=e^(0.05t)`

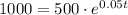
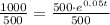
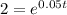
Take natural log of both sides:

`\text{ln}(2)=\text{ln}(e^(0.05t))`

`\text{ln}(2)=0.05t\cdot \text{ln}(e)`

`0.6931471805599453=0.05t\cdot 1`

`(0.6931471805599453)/(0.05)=(0.05t)/(0.05)`

`13.8629436=t`

`t\approx 13.9`

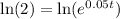
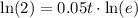
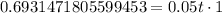
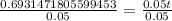
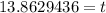
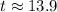
Therefore, it will take 13.9 years for Suzie's money to double and option 'c' is the correct choice.