Answer:
a)

b)
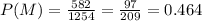
c)
Explanation:
For this case we have a total of 1254 people. 672 are women and 582 are female.
We know that 124 women wnat on to graduate school.
And 198 male want on to graduate school
We can define the following events:
F = The alumnus selected is female
M= The alumnus selected is male
A= Female and attend graduate school
And we can find the probabilities required using the empirical definition of probability like this:
Part a

Part b
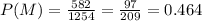
Part c
For this case we find the probability for the event A: The student selected is female and did attend graduate school
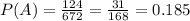
And using the complement rule we find P(A') representing the probability that the female selected did not attend graduate school like this: