Answer:
x = - 2
y = - 4
Explanation:
The given equations are:
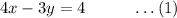

To solve this system of equations, we eliminate one variable.
Let us eliminate the variable 'x' here.
To do that multiply Equation (2) by 4.
⇒ 4x - 4y = 8 . . . (3)
The co - effecients of x in both the equations are now same. Subtract the two equations.
(1) - (3) = -3y - (-4y) = 4 - 8
⇒ - 3y + 4y = - 4
⇒ y = - 4
Substituting the value of 'y' in Equation (2) we get:
x - (-4) = 2
⇒ x + 4 = 2
⇒ x = - 2 which is the required answer.
Hence (x, y) = (-2, - 4) is the solution to the above system of equations.