Question

An urn contains 4 balls numbered 0 through 3. One ball is selected at random and removed from the urn and not replaced. All balls with nonzero numbers less than that of the selected ball are also removed from the urn. Then a second ball is selected at random from those remaining in the urn. What is the probability that the second ball selected is numbered 3?

A. {1}{4}.
B. {7}{24}.
C. {1}{3}.
D. {13}{24}.
E. {960}{7^5}.

Answer 1

The correct option is B)
`(7)/(24)`.

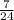Explanation:

Consider the provided information.

An urn contains 4 balls numbered 0 through 3. One ball is selected at random and removed from the urn and not replaced.

Case I: If first ball is 0 and 2nd ball is 3.

The probability is:
`(1)/(4) *(1)/(3)`

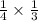
Case II: If first ball is 1 and 2nd ball is 3.

The probability is:
`(1)/(4) *(1)/(3)`

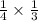
Case III: If first ball is 2 and 2nd ball is 3.

All balls with nonzero numbers less than that of the selected ball are also removed from the urn.

That means if we get 2 number ball then we will remove 1 number ball.

The probability is:
`(1)/(4) *(1)/(2)`

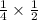
Case IV: If first ball is 3 then there is no 3 number ball.

The probability is:
`(1)/(4) *0`

Thus, the total number of ways are:

`\begin{aligned}(1)/(4) *(1)/(3)+(1)/(4) *(1)/(3)+(1)/(4) *(1)/(2)&=(1)/(12)+(1)/(12)+(1)/(8)\\&=(2+2+3)/(24)\\&=(7)/(24)\end{aligned}`

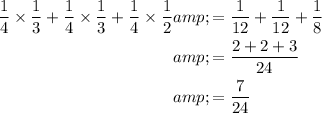
Hence, the correct option is B)
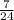`(7)/(24)`.