Question

Suppose f'(7)=9 and g(7)= 5.
Find h'(7) where h(x) = 3f(x) + 2g(x) + 7

h'(7)=???

Answer 1

The value of h'(7) = 44 .

Explanation:

Given:

f'(7)=9 and g(7)= 5

We have to find : h'(7)

Also,

⇔
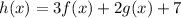`h(x) = 3f(x) + 2g(x) + 7` ...equation (i)

Plugging the value of 'x' = 7 in equation (i) the equation can be re-framed as:

⇔
`h(7) = 3f(7) + 2g(7) + 7`

⇔
`h(7) = 3f(7) + 2g(7) + 7`

Now plugging the value of f'=(7)=9 and g(7)=5 in the above equation:

⇔
`h(7) = 3(9) + 2(5) + 7`

⇔
`h(7)=27+10+7`

⇔
`h(7)=44`

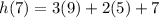
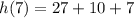
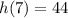
So the value of h=(7) = 44 .