Question

What is the distance between (-2, 4) and (5, 4) on a coordinate grid?

Answer 1

7 units

Explanation:

(Background info, skip if not interested or needed for you)

The equation for distance on a cartesian plane coordinate system is based off the pythagorean theorem.

`a^2 + b^2 = c^2`

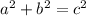
a and b being sides of a right triangle, c being the hypotenuse.

When we are solving for distance we are solving for c essentially.

`c` =
`√(a^2 + b^2)`

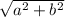
Because a and b are side lengths of the right triangle, we need to find a way to find that in terms of coordinates. So here we might say that a is equal to the horizontal distance between the 2 points or Δx, and we would say that b is the vertical distance between the 2 points Δy.

(solutions)

So essentially distance is:

`d = √((x_2 - x_1)^2+ (y_2-y_1)^2 )`

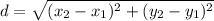
Now we just use the values given to us, and sub in the x and y values respectively.

(-2,4)
`x_1 = -2, y_1 = 4`

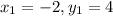
(5,4)
`x_2 = 5, y_2 = 4`

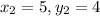
plug these values in:

`d = √(((5) - (-2))^2+ (4-4)^2 ) = √((7)^2+ (0)^2 ) = √(7^2 ) = 7`

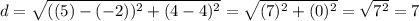
Therefore the distance is 7 units.