Question

There were 820 orange buttons in a container. The number of orange buttons was 160 fewer than the number of yellow buttons and 210 more than the number of green buttons. 1/3 of the total number of buttons in the container were blue buttons. How many buttons were there altogether?

Answer 1

Answer: There are 3615 buttons

Explanation:

From this situation we can write a system of equations if we tag the orange buttons with
`o`, the yellow buttons with
`y`, the green buttons with
`g` and the blue buttons with
`b`:

There were 820 orange buttons:

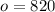`o=820` (1) Number of orange buttons

The number of orange buttons was 160 fewer than the number of yellow buttons:

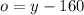`o=y-160` (2)

The number of orange buttons was 210 more than the number of green buttons:

`o=g+210` (3)

1/3 of the total number of buttons in the container were blue buttons:

If the total is the sum of the buttons of each color, we have:

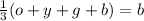`(1)/(3)(o+y+g+b)=b` (4)

At this point we have our system with 4 equations and 4 unknowns.

Let's begin by substituting (1) in (2):

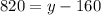`820=y-160` (5)

Isolating
`y`:

`y=980` (6) Number of yellow buttons

Subsituting (1) in (3):

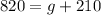`820=g+210` (7)

Isolating
`g`:

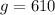`g=610` (8) Number of green buttons

Substituting (1), (6) and (8) in (4):

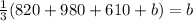`(1)/(3)(820+980+610+b)=b` (9)

Isolating
`b`:

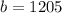`b=1205` (10) Number of blue buttons

Now we can find the total number of buttons:

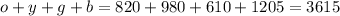`o+y+g+b=820+980+610+1205=3615` (11) This is the total number of buttons