Question

WHAT IS THE VALUE IF X???‼️‼️ HELP ASAP

Answer 1

The value of x is 40.

Solution:

Given ΔVDG and ΔVNG are similar triangles.

DG = 207, NQ = 138, GQ = 60, QV = x

To find the value of x.

In two triangles are similar, then the measures of the corresponding sides are in proportional to each other.

`$\Rightarrow(DG)/(NQ)=(GQ)/(QV)`

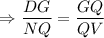
Substitute the given values.

`$ \Rightarrow(207)/(138)=(60)/(x)`

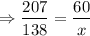
Do cross multiplication, we get

`$ \Rightarrow{207* x}=138*60`

`$ \Rightarrow{207* x}=8280`

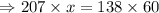
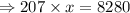
Divide by 207 on both sides of the equation, we get

`$ \Rightarrow x=(8280)/(207)`

`$ \Rightarrow x=40`

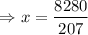
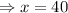
Hence the value of x is 40.