Question

the combined age of april and laura is 23 years. laura's age is two years more than half of april's age. what is laura's age

Answer 1

Laura's age is 9 years.

Solution:

Let x be the age of April.

Laura's age = 2 years more than half of April's age

Convert statement into algebraic expression:

Half of April's age =
`(x)/(2)`

2 years more than half of April's age =
`(x)/(2)+2`

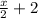
Combined age of April and Laura = 23

⇒ April's age + Laura's age = 23

`$\Rightarrow \ \ x+((x)/(2)+2) =23`

`$\Rightarrow \ \ x+(x)/(2)+2 =23`

`$\Rightarrow \ \ (x)/(1)+(x)/(2)+(2)/(1) =23`

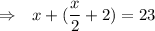
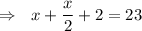
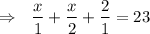
To add the fractions make the denominators same.

Multiplying 2 on both numerator and denominator of unlike terms, we get

`$\Rightarrow \ \ (x*2)/(1*2)+(x)/(2)+(2*2)/(1*2) =23`

`$\Rightarrow \ \ (2x)/(2)+(x)/(2)+(4)/(2) =23`

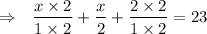
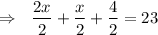
Denominators are same, now add the fractions.

`$\Rightarrow \ \ (2x+x+4)/(2) =23`

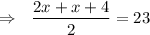
Do cross multiplication.

`$\Rightarrow \ \ 2x+x+4=23*2`

`$\Rightarrow \ \ 3x=46-4`

`$\Rightarrow \ \ 3x=42`

`$\Rightarrow \ \ x=14`

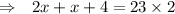
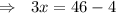
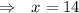
Aprils's age = 14 years

Laura's age =
`(14)/(2)+2`

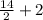
= 7 + 2

Laura's age = 9

Hence Laura's age is 9 years.