Answer: a. 0.58
b. 0.0256
c. (0.5494, 0.6006)
d. (0.5445, 0.6055)
Explanation:
Let p be the proportion of the respondents lack confidence they will be able to afford health insurance in the future.
As per given , Sample size : n= 1007
Sample proportion of respondents lack confidence they will be able to afford health insurance in the future:

a. The sample proportion gives the best estimate to the population proportion.
∴ The point estimate of the population proportion of adults who lack confidence they will be able to afford health insurance in the future =0.575 ≈0.58
b. Margin of error :
 , where z* =criticalz-value.
, where z* =criticalz-value.
For 90% confidence , z*= 1.645 ( By z-table)
Then ,
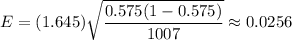
∴ the margin of error at 90% confidence is 0.0256 .
c. 90% confidence interval for p =
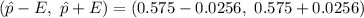
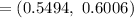
∴a 90% confidence interval for the population proportion of adults who lack confidence they will be able to afford health insurance in the future. (0.5494, 0.6006) .
d. For 95% confidence , z*= 1.96 ( By z-table)
Margin of error :
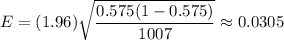
95% confidence interval for p =

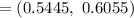
∴a 95% confidence interval for this population proportion=(0.5445, 0.6055)