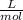Answer:
Units of a =

Units of b =
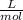
Step-by-step explanation:
The Van der Waal's equation is:-
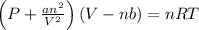
Where,
P is the pressure
V is the volume
n is the number of moles
T is the temperature
R is Gas constant having value
a and b are van der Waal's constant
If pressure is taken in atm and volume in L. So,
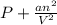 represents the pressure correction term. Then,
represents the pressure correction term. Then,
Units of a =

 represents the volume correction term. Then,
represents the volume correction term. Then,
Units of b =