Question

The cart is initially at rest. Force

F is applied to the cart for time ? t, after which the car has speed v. Suppose the same force is applied for the same time to a second cart with twice the mass. Friction is negligible. Afterward, the second cart's speed will be
a) 2v
b) 1/2v
c) v
d) 4v
e) 1/4v

Answer 1

`v'=(1)/(2)v`

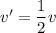
Step-by-step explanation:

Given that,

Initial speed of the cart, u = 0

Let F force is applied to the cart for time
`\Delta t` after which the car has speed v. The force on an object is given by :

F = ma

m is the mass of the cart

We need to find the speed of second cart, if the same force is applied for the same time to a second cart with twice the mass. Force becomes,

`F=(mv')/(t)`

`v'=(F t)/(2m)`

`v'=(1)/(2)v`

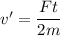
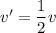
So, the speed of second cart is half of the initial speed of first cart. So, the correct option is (b).