Question

Two solid spheres, one of radius R and mass M, the other of radius 2R and mass 8M, roll down an incline. They start together from rest at the top of the incline. Which one will reach the bottom of the incline first?

A) The small sphere
B) The large sphere
C) Depends on ramp length
D) Both reach the bottom together.
E) It depends on the height of the incline

Answer 1

Step-by-step explanation:

Given

mass of first sphere is M and radius R

Mass of other sphere is 8 M and radius 2 R

acceleration of a rolling body in an inclined plane is given by

`a=(g\sin \theta )/(1+(I)/(mR^2))`

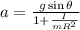
where I=moment of Inertia

m=mass of object

R=radius of object

`\theta`=inclination of plane

Moment of inertia of first body
`I=(2)/(5)MR^2`

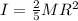
Moment of inertia other body
`I'=(2)/(5)(8M)(2R)^2=(64)/(5)MR^2`

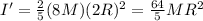
acceleration of first body
`a_1=(g\sin \theta )/(1+((2)/(5)MR^2)/(MR^2))`

`a_1=(5)/(7)g\sin \theta`

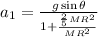
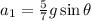
acceleration of second body
`a_2=(g\sin \theta )/(1+((64)/(5)MR^2)/(8M(2R)^2))`

`a_2=(g\sin \theta )/(1+(2)/(5))`

`a_2=(5)/(7)g\sin \theta`

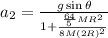
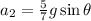
thus acceleration of first and second is same therefore they will reach at the same time