Answer:
Option B.
Explanation:
Given information: Circle G is inscribed with triangle EFD, arcED=104°.
We need to find the measure of arc ECF.
Draw a diagram by the given information.
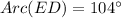 (Given)
(Given)
 (Central angle theorem)
(Central angle theorem)
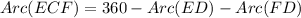
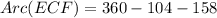
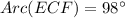
The measure of arc EDF is 98°.
Therefore, the correct option is B.