Question

Suppose that several insurance companies conduct a survey. They randomly surveyed 350 drivers and found that 280 claimed to always buckle up. We are interested in the population proportion of drivers who claim to always buckle up. (.20) n = (.20) p' = (.20) The standard deviation for sp = (.20) The z value for a 95% confidence interval is = (.20) Construct a 95% confidence interval for the population proportion that claim to always buckle Fill in the blanks to clarify the following diagram. LL (lower limit) = UL (upper limit) =

Answer 1

Lower limit = 0.76

Upper limit = 0.84

Explanation:

We are given the following in the question:

Sample size, n = 350

Number of drivers that buckle = 280

Formula:

`p' = (x)/(n) = (280)/(350) = 0.8`

`q' = 1-p' = 1 - 0.8 = 0.2`

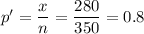
The standard deviation for sp =

`=\sqrt{\displaystyle(p'q')/(n)}\\\\=\sqrt{(0.8* 0.2)/(350)} = 0.02138`

95% Confidence Interval:

`p' \pm z_(critical)(s_p)`

`z_(critical)\text{ at}~\alpha_(0.05) = \pm 1.96`

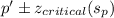
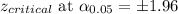
Putting the values, we get,

`0.8 \pm 1.96(0.02138)\\= 0.8 \pm 0.0419048\\=(0.7580952, 0.8419048)\\\approx (0.76,0.84)`

Lower limit = 0.76

Upper limit = 0.84