Question

In the following situation, determine whether you are asked to determine the number of permutations or combinations. Then

do the calculation.
How many ways are there to pick a subset of 3 different letters from the 26-letter alphabet?
a Combination; 23C3 = 1771
b. Permutation; 23P3 = 10626
C. Permutation; 26P3 = 15600
d. Combination; 26C3 = 2600


ASAP ! TAKING A TEST

Answer 1

The correct option is d.) 26C3 = 2600

Explanation:

How many ways are there to pick a subset of 3 different letters from the 26-letter alphabet?

This a selection problem therefore we will use combination.

Therefore to pick a subset of 3 different letters from the 26 letter alphabet is given by

`\binom{26}{3} = (26!)/(3!*(26-3)!) = (26*25*24)/(6) = 2600`

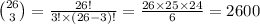
Therefore the correct option is d.) 26C3 = 2600